Problem 1 - cΒΆ

Given conditions: \(U\) = 0, \(\Gamma\) = 0.1 + 0.1 \(\phi\), and \(N\) = 20.

  1. Find \(\phi\) using TDMA for following \(Q\) and corresponding exact solution cases:
  • About solution method
    • Compared to the problem 1-b, this is non-linear problem because the diffusivity is dependent on the solution \(\phi\). For this reason, it can’t be solved with simple block iterative method like TDMA. The reason is because we cannot build tri-diagonal \(A\) matrix for this case due to the non-linear behavior.
    • The solution method for this problem has to be iterative method to track the converging solution.
    • The iterative method updates the initial guess of solution space and seeks the converged value by repeating the numerical algorithm.
    • Initially \(\phi_{i}\) space is initialized with certain value. Here, every points is initialized with zero.
    • Then, the every step of TDMS method will propagate the updated info from the guessed \(\phi\).
    • The code has a function to check the residual value from the updated \(\phi\) and quantify how much it propagates from the solution of previous step.
    • It repeats until the deviation of solution from the past reaches to zero level. (NOTE: the residual will never reach to zero level because of truncation errors of our finite difference equations)

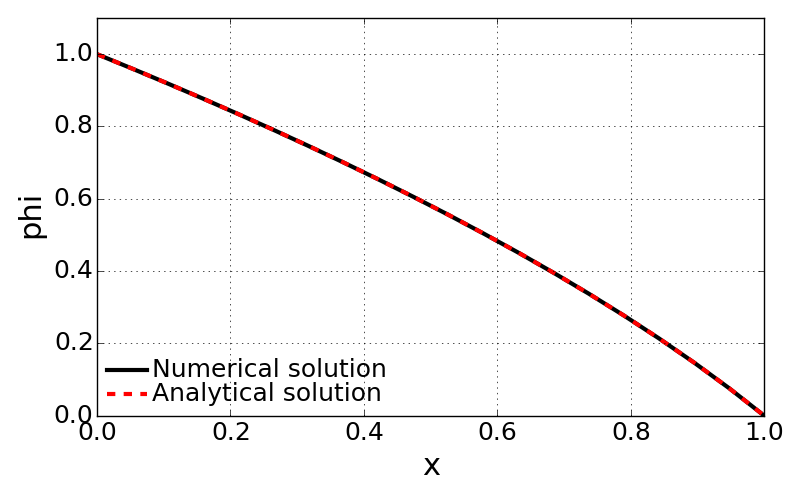
  • CASE1: \(Q = 0\), \(\;\; \phi(x) = -1+\sqrt{4-3x}\)

    ../../_images/pr1c_case1.png
    • Converged at 5th iterations with residual of 0.000876728469266
    • Average error = 9.0129271003e-06
    • Calculation time [sec] = 0.001337

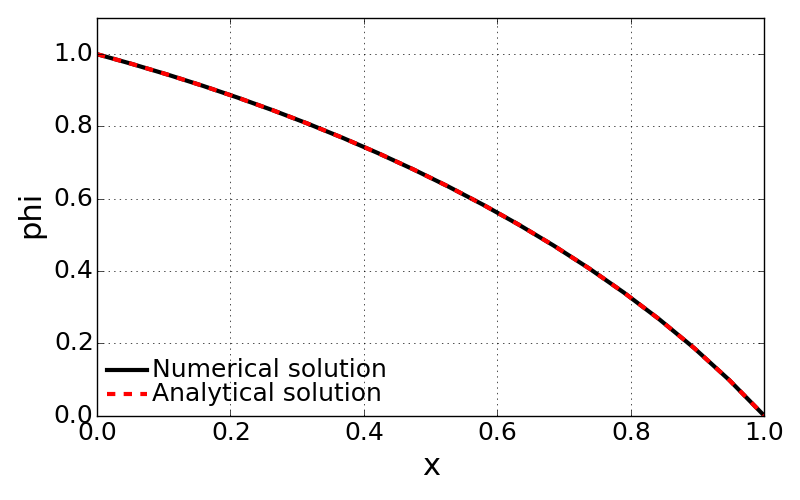
  • CASE2: \(Q = 0.1\), \(\;\; \phi(x) = -1+\sqrt{4-2x-x^{2}}\)

    ../../_images/pr1c_case2.png
    • Converged at 5th iterations with residual of 0.000716942145114
    • Average error = 1.01159413052e-05
    • Calculation time [sec] = 0.001383

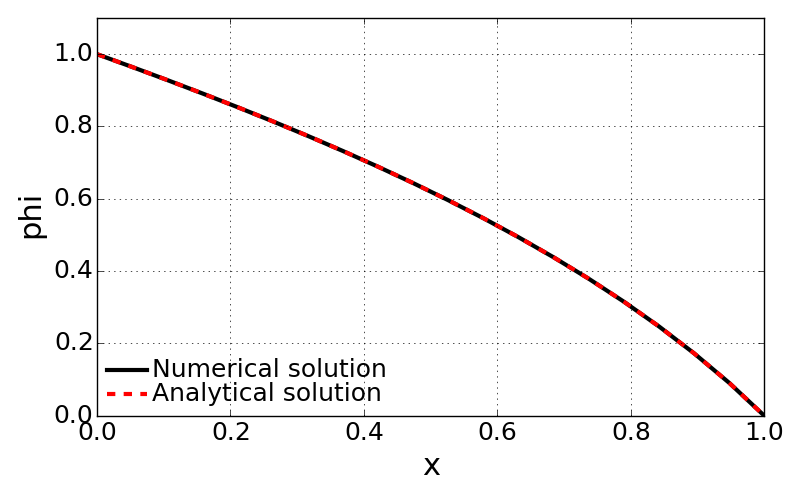
  • CASE3: \(Q = 0.1x\), \(\;\; \phi(x) = -1+\sqrt{4-(8/3)x - x^{3}/3}\)

    ../../_images/pr1c_case3.png
    • Converged at 5th iterations with residual of 0.000707116960016
    • Average error = 8.99517612803e-06
    • Calculation time [sec] = 0.001404

  • Discussions on comparison between different source terms
    • Only difference between these three cases has come from the source term deviation.
    • Since we set \(U\) to zero, we do not expect any convective effect. Only matter of the problem is diffusion and source terms.
    • Pure diffusion problem with constant diffusivity will result in linear \(\phi\) profile along the x-direction.
    • The slight bump from the pure diffusion problem is a combination of non-linear diffusivity and the source terms like heat source in heat conduction problem.
    • The CASE 1 represents the pure diffusion problem with non-linear diffusivity. Since the diffusivity is proportional to \(\phi\), higher value of \(\phi\) is more likely to propage to the lower \(\phi\) region.
    • CASE 2 and CASE 3 are showing source term effect. When the heat conduction with heat source is imagined, temperature rises with the heat source.
    • CASE 3 has less heat source as it goes far away from the origin. It then leads to less bump compared to the CASE 2.

  1. Comparison in calculation time
  calculation time total # of iterations
0.000417 1
  1. CASE 1
 0.001337 5
  1. CASE 2
 0.001383 5
  1. CASE 3
 0.001404 5
  • Discussion
    • As discussed earlier, the previous problem 1-b was a linear set of equations. So it can be solved with linear system of equations using block iterative method called here TDMA.
    • So, the TDMA in problem 1-b was not iterated multiple times.
    • The non-linear problem here is asking us to seek the converged solution with iterative method.
    • Three differenct source terms cases requires only 5 iterations until it satifies the convergence criteria. Here, convergence criteria was set to 0.001.
    • Since the solution method is identical, the calculation time is almost identical because it proceeds same repetition of TDMA 5 times.
    • Slight change of calculation time might have come from the compute resource occupied by the other software.